LeetCode(111-120)
111. Minimum Depth of Binary Tree¶
- Tree
- Depth-first Search
- Breadth-first Search
Given a binary tree, find its minimum depth.
The minimum depth is the number of nodes along the shortest path from the root node down to the nearest leaf node.
Note: A leaf is a node with no children.
Example:
Given binary tree
[3,9,20,null,null,15,7],
return its minimum depth = 2.
Solution
此题思路同求二叉树的深度,LC-104-Maximum Depth of Binary Tree。
Runtime 0 ms
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public int minDepth(TreeNode root) {
if (root == null) return 0;
if (root.left == null && root.right == null) return 1;
int left = root.left == null ? Integer.MAX_VALUE : minDepth(root.left);
int right = root.right == null ? Integer.MAX_VALUE : minDepth(root.right);
return Math.min(left, right) + 1;
}
}
112. Path Sum¶
- Tree
- Depth-first Search
Given a binary tree and a sum, determine if the tree has a root-to-leaf path such that adding up all the values along the path equals the given sum.
Note: A leaf is a node with no children.
Example:
Given the below binary tree and
sum = 22,
return true, as there exist a root-to-leaf path
5->4->11->2which sum is 22.
Solution
Runtime 0 ms
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
// fucking test case: [] 0
public boolean hasPathSum(TreeNode root, int sum) {
if (root == null) return false;
return hasPathSumInner(root, sum);
}
private boolean hasPathSumInner(TreeNode root, int sum) {
sum -= root.val;
if (root.left != null || root.right != null) {
boolean flag = false;
if (root.left != null) {
flag = hasPathSumInner(root.left, sum);
}
if (!flag && root.right != null) {
flag = hasPathSumInner(root.right, sum);
}
return flag;
} else {
return sum == 0;
}
}
}
113. Path Sum II¶
- Tree
- Depth-first Search
Given a binary tree and a sum, find all root-to-leaf paths where each path's sum equals the given sum.
Note: A leaf is a node with no children.
Example:
Given the below binary tree and
sum = 22,
Return:
[
[5,4,11,2],
[5,8,4,5]
]
Solution
Runtime 1 ms
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public List<List<Integer>> pathSum(TreeNode root, int sum) {
List<List<Integer>> result = new ArrayList<>();
List<Integer> solution = new ArrayList<>();
if (root == null) return result;
pathSum(root, sum, solution, result);
return result;
}
private void pathSum(TreeNode root, int sum, List<Integer> solution, List<List<Integer>> result) {
sum -= root.val;
solution.add(root.val);
if (root.left == null && root.right == null && sum == 0) {
result.add(new ArrayList<>(solution));
solution.remove(solution.size() - 1);
return;
}
if (root.left != null) {
pathSum(root.left, sum, solution, result);
}
if (root.right != null) {
pathSum(root.right, sum, solution, result);
}
solution.remove(solution.size() - 1);
}
}
114. Flatten Binary Tree to Linked List¶
- Tree
- Depth-first Search
Given a binary tree, flatten it to a linked list in-place.
For example, given the following tree:
The flattened tree should look like:
Solution
观察一下给的示例,我们发现可以在树的前序遍历过程中进行操作,得到最后的结果。具体操作在第18~22行。
Runtime 0 ms
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
private TreeNode head;
public void flatten(TreeNode root) {
if (root == null) return;
TreeNode p = root.left;
TreeNode q = root.right;
if (head != null) {
head.right = root;
}
root.left = null;
head = root;
flatten(p);
flatten(q);
}
}
115. Distinct Subsequences¶
- String
- Dynamic Programming
Given a string S and a string T, count the number of distinct subsequences of S which equals T.
A subsequence of a string is a new string which is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (ie,
"ACE"is a subsequence of"ABCDE"while"AEC"is not).
Example 1:
Input: S = "rabbbit", T = "rabbit"
Output: 3
Explanation:
As shown below, there are 3 ways you can generate "rabbit" from S.
(The caret symbol ^ means the chosen letters)
rabbbit
^^
rabbbit
^
rabbbit
^^ ^
Example 2:
Input: S = "babgbag", T = "bag"
Output: 5
Explanation:
As shown below, there are 5 ways you can generate "bag" from S.
(The caret symbol ^ means the chosen letters)
babgbag
^^
babgbag
^
babgbag
babgbag
^ ^^
babgbag
^
Solution
两个字符串问题,解法要不是HashTable + Two Pointers,要不就是Dynamic Programming。很显然,本次使用动态规划是没有错的。
通过上面两个示例的动态规划过程,可以得到下面的表达式:
解释如下: 1. 如果当前比较的两个字符不相等,即T[i] != S[j],那么当前的结果为T[0...i]与S[0...j-1]的结果,即dp(i, j - 1) 2. 如果两个字符相等,那么当前的结果显然需要先加上两个字符串前一位的结果,即dp(i - 1, j - 1),然后考虑一下T中新增的字符,我们需要以这个T[0...i]整体在S[0...j-1]中去进行匹配,这个结果就是dp(i, j - 1)。
比如在第二个例子,T[0...i-1]为*b*,S[0...j-1]为*babgb*,T[i]=S[j]=a
那么dp(i - 1, j - 1)就是ba与babgba的结果:
b a b g b a
b x x x x a -> 1
b a b g b a
x x b x x a -> 2
b a b g b a
x x x x b a -> 3
dp(i, j - 1)的意思就是ba在babgb中的结果:
b a b g b
b a x x x -> 4
所以,结果为4。
Runtime 3 ms
class Solution {
public int numDistinct(String s, String t) {
final int n = s.length();
final int m = t.length();
int[][] dp = new int[m + 1][n + 1];
for (int i = 0; i <= n; i++) {
dp[0][i] = 1;
}
char[] ss = s.toCharArray();
char[] ts = t.toCharArray();
for (int i = 1; i <= m; i++) {
for (int j = i; j <= n; j++) {
if (ss[j - 1] == ts[i - 1]) {
dp[i][j] = dp[i - 1][j - 1] + dp[i][j - 1];
} else {
dp[i][j] = dp[i][j - 1];
}
}
}
return dp[m][n];
}
}
116. Populating Next Right Pointers in Each Node¶
- Tree
- Depth-first Search
You are given a perfect binary tree where all leaves are on the same level, and every parent has two children. The binary tree has the following definition:
Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to
NULL.Initially, all next pointers are set to
NULL.
Example:
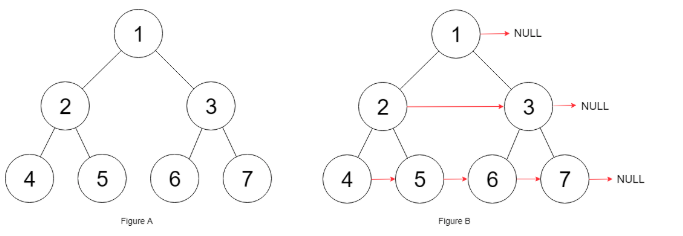
Input: {"$id":"1","left":{"$id":"2","left":{"$id":"3","left":null,"next":null,"right":null,"val":4},"next":null,"right":{"$id":"4","left":null,"next":null,"right":null,"val":5},"val":2},"next":null,"right":{"$id":"5","left":{"$id":"6","left":null,"next":null,"right":null,"val":6},"next":null,"right":{"$id":"7","left":null,"next":null,"right":null,"val":7},"val":3},"val":1}
Output: {"$id":"1","left":{"$id":"2","left":{"$id":"3","left":null,"next":{"$id":"4","left":null,"next":{"$id":"5","left":null,"next":{"$id":"6","left":null,"next":null,"right":null,"val":7},"right":null,"val":6},"right":null,"val":5},"right":null,"val":4},"next":{"$id":"7","left":{"$ref":"5"},"next":null,"right":{"$ref":"6"},"val":3},"right":{"$ref":"4"},"val":2},"next":null,"right":{"$ref":"7"},"val":1}
Explanation: Given the above perfect binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B.
Note:
- You may only use constant extra space.
- Recursive approach is fine, implicit stack space does not count as extra space for this problem.
Solution
此题如果没有要求O(1)的空间复杂度的话,是可以使用队列来完成的,这就变成了一个树的层序遍历算法。然而,本题不使用这种方式,下面的进阶题使用树的层序遍历算法来求解。
回到本题,我们想一下,如果该层的右指针已经全部确定完毕,如何确定下一层的呢?
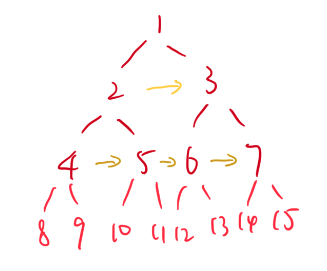
如上图所示,我们只需要
- 先将当前节点的左节点的next指针指向当前节点的右节点
- 如果当前节点有next节点,再将当前节点的右节点的next指针指向当前节点的next节点的左节点
- 当前节点指向当前节点的next节点,如此迭代即可完成下一层
Runtime 0 ms
/*
// Definition for a Node.
class Node {
public int val;
public Node left;
public Node right;
public Node next;
public Node() {}
public Node(int _val,Node _left,Node _right,Node _next) {
val = _val;
left = _left;
right = _right;
next = _next;
}
};
*/
class Solution {
public Node connect(Node root) {
if (root == null) return root;
Node pre = root;
Node cur = null;
while (pre.left != null) {
cur = pre;
while (cur != null) {
cur.left.next = cur.right;
if (cur.next != null) cur.right.next = cur.next.left;
cur = cur.next;
}
pre = pre.left;
}
return root;
}
}
117. Populating Next Right Pointers in Each Node II¶
- Tree
- Depth-first Search
You are given a perfect binary tree where all leaves are on the same level, and every parent has two children. The binary tree has the following definition:
Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to
NULL.Initially, all next pointers are set to
NULL.
Example:
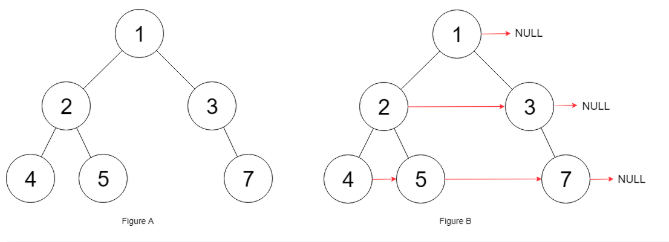
Input: {"$id":"1","left":{"$id":"2","left":{"$id":"3","left":null,"next":null,"right":null,"val":4},"next":null,"right":{"$id":"4","left":null,"next":null,"right":null,"val":5},"val":2},"next":null,"right":{"$id":"5","left":null,"next":null,"right":{"$id":"6","left":null,"next":null,"right":null,"val":7},"val":3},"val":1}
Output: {"$id":"1","left":{"$id":"2","left":{"$id":"3","left":null,"next":{"$id":"4","left":null,"next":{"$id":"5","left":null,"next":null,"right":null,"val":7},"right":null,"val":5},"right":null,"val":4},"next":{"$id":"6","left":null,"next":null,"right":{"$ref":"5"},"val":3},"right":{"$ref":"4"},"val":2},"next":null,"right":{"$ref":"6"},"val":1}
Explanation: Given the above binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B.
Note:
- You may only use constant extra space.
- Recursive approach is fine, implicit stack space does not count as extra space for this problem.
Solution
此题如果没有要求O(1)的空间复杂度的话,是可以使用队列来完成的,这就变成了一个树的层序遍历算法。然而,本题使用了这种方式。因为够简单,无脑。
实际上,基于上一题的解法,我们只需要在链接两个节点的时候,判断左右节点是否为空,再根据情况处理即可,思路和上题的一样。但是没有多少意义,所以这里采用了层序遍历的算法,该解法可以适用于该题和上一题。
Runtime 2 ms
/*
// Definition for a Node.
class Node {
public int val;
public Node left;
public Node right;
public Node next;
public Node() {}
public Node(int _val,Node _left,Node _right,Node _next) {
val = _val;
left = _left;
right = _right;
next = _next;
}
};
*/
class Solution {
public Node connect(Node root) {
if (root == null || (root.left == null && root.right == null)) return root;
Queue<Node> queue = new LinkedList<>();
queue.offer(root);
int count = 0;
int rest = 1;
Node prev = null;
while (!queue.isEmpty()) {
Node node = queue.poll();
if (node.left != null) {
queue.offer(node.left);
count++;
}
if (node.right != null) {
queue.offer(node.right);
count++;
}
if (prev != null) {
prev.next = node;
}
prev = node;
if (--rest == 0) {
rest = count;
count = 0;
prev = null;
}
}
return root;
}
}
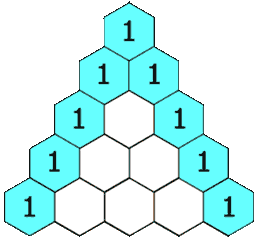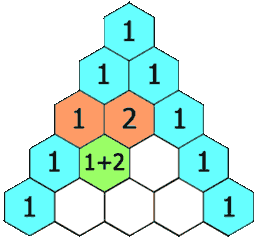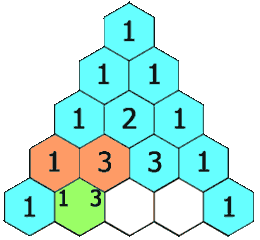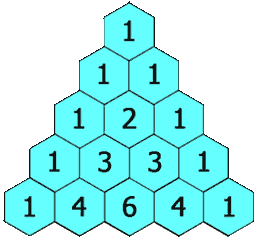
118. Pascal's Triangle¶
- Array
Given a non-negative integer numRows, generate the first numRows of Pascal's triangle.
In Pascal's triangle, each number is the sum of the two numbers directly above it.
Example:
Input: 5
Output:
[
[1],
[1,1],
[1,2,1],
[1,3,3,1],
[1,4,6,4,1]
]
Solution
Pascal三角就是杨辉三角,此题没什么需要注意的。
Runtime 0 ms
class Solution {
public List<List<Integer>> generate(int numRows) {
List<List<Integer>> result = new ArrayList<>();
if (numRows < 1) return result;
for (int i = 1; i <= numRows; i++) {
List<Integer> row = new ArrayList<>(i);
row.add(1);
for (int j = 2; j <= i; j++) {
if (j == i) {
row.add(1);
} else {
List<Integer> prev = result.get(i - 2);
row.add(prev.get(j - 2) + prev.get(j - 1));
}
}
result.add(row);
}
return result;
}
}
119. Pascal's Triangle II¶
- Array
Given a non-negative index k where k ≤ 33, return the \(k^{th}\) index row of the Pascal's triangle.
Note that the row index starts from 0.
In Pascal's triangle, each number is the sum of the two numbers directly above it.
Example:
Input: 3
Output: [1,3,3,1]
Follow up:
Could you optimize your algorithm to use only O(k) extra space?
Solution
Pascal三角就是杨辉三角,此题有一个Follow up,需要使用O(k)的空间复杂度。言外之意就是说,中间的计算过程只能使用一个一维数组进行。
考虑到从前往后计算某一层的结果时,上一层的结果会被覆盖掉,而我们又需要上一层的结果,所以从后往前计算就好了。而且,三角中的数字会呈对称的形式进行排布,所以只需要计算一半,另外一半进行复制即可。
Runtime 0 ms
class Solution {
public List<Integer> getRow(int rowIndex) {
int[] solution = new int[rowIndex + 1];
Arrays.fill(solution, 1);
for (int i = 2; i <= rowIndex; i++) {
for (int j = i / 2; j >= 1; j--) {
solution[j] += solution[j - 1];
}
for (int j = i / 2 + 1; j < i; j++) {
solution[j] = solution[i - j];
}
}
List<Integer> result = new ArrayList<>(solution.length);
for (int num : solution) {
result.add(num);
}
return result;
}
}
120. Triangle¶
- Array
- Dynamic Programming
Given a triangle, find the minimum path sum from top to bottom. Each step you may move to adjacent numbers on the row below.
For example, given the following triangle
[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]The minimum path sum from top to bottom is
11(i.e., 2 + 3 + 5 + 1 = 11).
Note:
Bonus point if you are able to do this using only O(n) extra space, where n is the total number of rows in the triangle.
Solution
本题可以使用动态规划求解,由于是求的路径,所以每一个点最多与上一层的两个点接触。这样可以求出一层层的路径和,最后在dp数组中找出最小值就是答案了。
Runtime 1 ms
class Solution {
public int minimumTotal(List<List<Integer>> triangle) {
if (triangle == null || triangle.size() == 0) return 0;
final int n = triangle.size();
int[] dp = new int[n];
dp[0] = triangle.get(0).get(0);
for (int i = 1; i < n; i++) {
List<Integer> row = triangle.get(i);
for (int j = row.size() - 1; j >= 0; j--) {
int min;
if (j == 0) {
min = dp[j];
} else if (j == row.size() - 1) {
min = dp[j - 1];
} else {
min = Math.min(dp[j - 1], dp[j]);
}
dp[j] = min + row.get(j);
}
}
int result = Integer.MAX_VALUE;
for (int num : dp) {
result = result > num ? num : result;
}
return result;
}
}