高质量的代码

规范性、完整性、鲁棒性。

1. 代码的完整性¶

从三个方面确保代码的完整性
通常我们可以从功能测试、边界测试和负面测试3个方面设计测试用例
3种错误处理方式
1. 函数返回值
2. 设置全局变量
3. 抛异常

下表是上述3种错误处理方式的优缺点：

	优点	缺点
返回值	和系统API一致	不能方便地使用计算结果
全局变量	能够方便地使用计算结果	用户可能忘记检查全局变量
异常	可以为不同的出错原因定义不同的异常类型，逻辑清晰明了	有些语言不支持异常，抛出异常时对性能有负面影响

1.1 (16)数值的整数次方¶

实现函数double Power(double base, int exponent)，求base的exponent次方。不得使用库函数，同时不需要考虑大数问题。

与LC-50-Pow(x, n)类似。不过LeetCode上需要注意n的溢出问题。

此题看起来简单，但却有一些情况需要考虑到。
首先需要考虑到指数为0或负数的情况。当指数为负数时，可以先对指数求绝对值，算出结果之后再取倒数。在求倒数的时候，如果底数是0怎么办，如何告诉函数的调用者出现了这种错误。
最后需要指出的是，由于0的0次方在数学上是没有意义的，因此无论输出是0还是1都是可以接受的，但这需要和面试官说清楚，表明我们已经考虑到这个边界值了。

全面的解法如下：

private boolean invalidInput;

private double power(double base, int exponent) {
    invalidInput = false;

    if (exponent < 0 && base == 0) {
        invalidInput = true;
        return 0;
    }

    long absExponent = Math.abs(exponent * 1L);

    double result = powerInner(base, absExponent);

    return exponent < 0 ? 1.0 / result : result;
}

private double powerInner(double base, long exponent) {
    double result = 1.0;

    for (int i = 1; i <= exponent; i++) {
        result *= base;
    }

    return result;
}

在上面的代码中，我们采用全部变量来标识是否出错了。如果出错了，则返回的值是0。但为了区分是出错的时候返回的0，还是底数为0的时候正常运行的0，我们定义了一个全局变量invalidInput。当出错的时候，这个变量被设为true，否则为false。

全面且高效的解法
如果输入的指数为32，我们需要在循环中做32次乘法。但我们可以考虑换一种思路：利用如下公式求a的n次方：

\[ a^n=\begin{cases} a^{n/2} \cdot a^{n/2}, & n为偶数 \\ a^{(n-1)/2} \cdot a^{(n-1)/2} \cdot a, & n为奇数 \end{cases} \]

我们在介绍用\(O(logn)\)时间求斐波那契数列时讨论过这个公式，这个公式很容易通过递归实现。新的powerInner方法如下所示：

private double powerInner(double base, long exponent) {
    if (exponent == 0) {
        return 1;
    } else if (exponent == 1) {
        return base;
    }

    double result = powerInner(base, exponent >> 1);
    result *= result;
    if ((exponent & 0x1) == 1) {
        result *= base;
    }

    return result;
}

这里用右移运算符代替了除以2，用位于运算代替了求余运算符来判断一个数是不是奇数。

1.2 (17)打印1到最大的n位数¶

输入数字n，按顺序打印出从1最大的n位十进制数。比如输入3，则打印出1、2、3一直到最大的3位数即999。

当输入的n很大时，我们求最大的n位数是不是用int或者long都会溢出。也就是说我们需要考虑大数问题。我们需要使用字符串模拟数字加法的解法。

使用字符串模拟数字加法

private void print1ToMaxOfNDigits_1(int n) {
    if (n <= 0) return;

    char[] number = new char[n];

    // 初始化字符串
    for (int i = 0; i < n; i++) {
        number[i] = '0';
    }

    while (!increment(number)) {
        printNumber(number);
    }
}

private boolean increment(char[] number) {
    boolean isOverflow = false;
    int takeOver = 0;
    int length = number.length;

    for (int i = length - 1; i >= 0; i--) {
        int sum = number[i] - '0' + takeOver;
        if (i == length - 1) {
            sum++;
        }

        if (sum >= 10) {
            // 累加有进位
            if (i == 0) {
                // 已经打印完毕了，设置为true，不在继续计数
                isOverflow = true;
            } else {
                // 还没有打印完毕，在后续循环中进行进位操作
                sum -= 10;
                takeOver = 1;
                number[i] = (char) (sum + '0');
            }
        } else {
            // 累加没有进位，直接结束循环
            number[i] = (char) ('0' + sum);
            break;
        }
    }

    return isOverflow;
}

// ====================公共函数====================
private void printNumber(char[] number) {
    boolean begin0 = true;
    for (char ch: number) {
        // 只需要略过打头的0
        if (begin0 && ch != '0') {
            begin0 = false;
        }
        if (!begin0) {
            System.out.print(ch);
        }
    }

    System.out.println();
}

解法二：数字排列解法，递归实现

上面的思路比较直观，戴氏代码有点长，在短短几十分钟时间内完整、正确地写出这么长的代码，不是一件容易的事情。
我们换一种思路考虑这个问题，如果我们在数字前面补0，就会发现n位所有十进制数其实就是n个从0到9的全排列。也就是说，我们把数字的每一位都从0到9排列一遍，就得到了所有的十进制数。只是在打印的时候，排在前面的0不打印出来罢了。

全排列用递归很容易实现，数字的每一位都可能是0到9中的一个数，然后设置下一位。递归结束的条件就是我们已经设置了数字的最后一位。

private void print1ToMaxOfNDigits_2(int n) {
    if (n <= 0) return;

    char[] number = new char[n];

    // 设置第0位
    for (int i = 0; i < 10; i++) {
        number[0] = (char) (i + '0');
        print1ToMaxOfNDigits_2_Recursively(number, n, 0);
    }
}

private void print1ToMaxOfNDigits_2_Recursively(char[] number, int length, int index) {
    // 已经设置了最后一位，直接打印即可
    if (index == length - 1) {
        printNumber(number);
        return;
    }

    // 设置第index+1位
    for (int i = 0; i < 10; i++) {
        number[index + 1] = (char) (i + '0');
        print1ToMaxOfNDigits_2_Recursively(number, length, index + 1);
    }
}

1.3 (18)删除链表的节点¶

1.3.1 在O(1)时间删除链表结点¶

给定单向链表的头指针和一个结点指针，定义一个函数在O(1)时间删除该结点。

常规的做法需要从头开始顺序查找，得到将要被删除的节点的前一个节点。
但是，在一般情况下，我们可以很方便地得到要删除节点的下一个节点。如果我们把下一个节点的内容复制到需要删除的节点上覆盖原有的内容，在把下一个节点删除，那就相当于把当前需要删除的节点删除了。
这个思路有一个问题：如果要删除的节点位于链表的尾部，那么它就没有下一个节点，这时仍然需要从头开始遍历，得到该节点的前序节点，然后完成删除操作。
最后需要注意的是，如果链表中只有一个节点，而我们又需要删除链表的头结点，那么此时我们在删除节点后，还需要链表的头结点设置为null。

总的时间复杂度是\([(n-1) \times O(1)+O(n)]/n\)，结果还是\(O(1)\)。但是这基于一个假设，要删除的节点的确在链表中。

private ListNode deleteNode(ListNode head, ListNode toBeDeleted) {
    if (head == null || toBeDeleted == null) {
        return null;
    }

    // 要删除的结点不是尾结点
    if (toBeDeleted.next != null) {
        toBeDeleted.value = toBeDeleted.next.value;
        toBeDeleted.next = toBeDeleted.next.next;
    } else if (head == toBeDeleted) {
        // 链表只有一个结点，删除头结点（也是尾结点）
        head = null;
    } else {
        // 链表中有多个结点，删除尾结点
        ListNode p = head;
        while (p.next != toBeDeleted) {
            p = p.next;
        }
        p.next = null;
    }

    return head;
}

1.3.2 删除链表中重复的结点¶

在一个排序的链表中，如何删除重复的结点？例如，在图3.4（a）中重复结点被删除之后，链表如图3.4（b）所示。

删除链表中重复的节点

注：(a)一个有7个节点的链表：1、2、3、3、4、4、5；(b)当重复的节点被删除之后，链表中只剩下3个节点。

弄一个头结点可以有效的规避边界问题。

private ListNode deleteDuplication(ListNode head) {
    if (head == null) {
        return null;
    }

    // 创建一个头结点
    ListNode rHead = new ListNode(0);
    rHead.next = head;

    ListNode p, q;
    p = rHead;

    while (p.next != null) {
        q = p.next;
        boolean duplicate = false;

        while (q.next != null && q.value == q.next.value) {
            duplicate = true;
            q = q.next;
        }

        if (duplicate) {
            p.next = q.next;
        } else {
            p = q;
        }
    }

    return rHead.next;
}

1.4 (19)正则表达式匹配¶

请实现一个函数用来匹配包含‘.’和‘*’的正则表达式。模式中的字符‘.’表示任意一个字符，而‘*’表示它前面的字符可以出现任意次（含0次）。在本题中，匹配是指字符串的所有字符匹配整个模式。例如，字符串“aaa”与模式“a.a”和“ab*ac*a”匹配，但与“aa.a”及“ab*a”均不匹配。

代码同LC-10-Regular Expression Matching。

在输入参数有效的情况下，先检查模式中第二个字符是不是'*'。

若不是，那么本次只需要比较字符串中第一个字符和模式中的第一个字符是否相匹配。若匹配，那么字符串和模式都向后移动一个字符，然后匹配剩余的字符串和模式。若不匹配，直接返回false。
若是'*',那么有两种匹配方式：
1. "aab"、"c*a*b"方式
  此时在模式上向后移动两个字符即可。
2. "aaa"、"a*a"方式
  此时如果第一个字符可以匹配，则在字符串上向后移动一个字符，模式保持不变即可。

代码Copy如下：

class Solution {
    public boolean isMatch(String text, String pattern) {
        if (pattern.isEmpty()) return text.isEmpty();
        boolean first_match = (!text.isEmpty() &&
                               (pattern.charAt(0) == text.charAt(0) || pattern.charAt(0) == '.'));

        if (pattern.length() >= 2 && pattern.charAt(1) == '*'){
            return (isMatch(text, pattern.substring(2)) ||
                    (first_match && isMatch(text.substring(1), pattern)));
        } else {
            return first_match && isMatch(text.substring(1), pattern.substring(1));
        }
    }
}

1.5 (20)表示数值的字符串¶

请实现一个函数用来判断字符串是否表示数值（包括整数和小数）。例如，字符串“+100”、“5e2”、“-123”、“3.1416”及“-1E-16”都表示数值，但“12e”、“1a3.14”、“1.2.3”、“+-5”及“12e+5.4”都不是。

此题和LC-65-Valid Number相识

表示数值的字符串遵循模式A[.[B]][e|EC]或者.B[e|EC]，其中A为数值的整数部分，B紧跟着小数点为数值的小数部分，C紧跟着e或者E，为数值的指数部分。在小数里可能没有数值的整数部分。例如，小数.123等于0.123。因此A部分不是必须的。如果一个数没有整数部分，那么它的小数部分不能为空。
上述A和C都是可能以+或者-开头的0~9的数位串；B也是0~9的数位串，但前面不能有正负号。
以表示数值的字符串"123.45e+6"为例，"123"就是A，"45"就是B，"+6"就是C。

private int index;

private boolean isNumeric(String str) {
    if (str == null) {
        return false;
    }

    return isNumeric(str.toCharArray());
}

private boolean isNumeric(char[] str) {
    index = 0;
    boolean numeric = scanInteger(str);

    // 如果出现'.'，接下来是数字的小数部分
    if (index < str.length && str[index] == '.') {
        index++;

        // 下面一行代码用||的原因：
        // 1. 小数可以没有整数部分，例如.123等于0.123；此时原来的numeric=false
        // 2. 小数点后面可以没有数字，例如233.等于233.0；此时原来的numeric=true
        // 3. 当然小数点前面和后面可以有数字，例如233.666；此时原来的numeric=true
        numeric = scanUnsignedInteger(str) || numeric;
    }

    // 如果出现'e'或者'E'，接下来跟着的是数字的指数部分
    if (index < str.length && (str[index] == 'e' || str[index] == 'E')) {
        index++;

        // 下面一行代码用&&的原因：
        // 1. 当e或E前面没有数字时，整个字符串不能表示数字，例如.e1、e1；此时原来的numeric=false
        // 2. 当e或E后面没有整数时，整个字符串不能表示数字，例如12e、12e+5.4；此时原来的numeric=true
        numeric = numeric && scanInteger(str);
    }

    return index == str.length && numeric;
}

private boolean scanInteger(char[] str) {
    if (index < str.length && (str[index] == '-' || str[index] == '+')) {
        index++;
    }
    return scanUnsignedInteger(str);
}

private boolean scanUnsignedInteger(char[] str) {
    int tmp = index;

    while (index < str.length && str[index] >= '0' && str[index] <= '9') {
        index++;
    }

    return index > tmp;
}

1.6 (21)调整数组顺序使奇数位于偶数前面¶

输入一个整数数组，实现一个函数来调整该数组中数字的顺序，使得所有奇数位于数组的前半部分，所有偶数位于数组的后半部分。

解法一：完成基本功能

该题只要求把奇数放在数组的前半部分，偶数放在数组的后半部分，因此所有的奇数应该位于偶数的前面。所以我们可以写出下面这段代码。

void reorderOddEven_1(int[] pData, int length) {
    if (pData == null || length == 0) {
        return;
    }

    int lo = 0, hi = length - 1;

    while (lo < hi) {
        // 向后移动lo，直到它指向偶数
        while (lo < hi && (pData[lo] & 0x1) != 0) {
            lo++;
        }

        // 向前移动hi，直到它指向奇数
        while (lo < hi && (pData[hi] & 0x1) == 0) {
            hi--;
        }

        if (lo < hi) {
            int temp = pData[lo];
            pData[lo] = pData[hi];
            pData[hi] = temp;
        }
    }
}

解法二：考虑可扩展性

我们需要提供解决一系列同类型题目的通用方法。这只需要替换方法中两处判断即可。
下面这段代码提供了一个参数并返回一个值的通用接口Function<P1, R>，在此接口上实现了一个IsEvenFunction用来解决具体问题。

/** A function that takes 1 argument. */
private interface Function<P1, R> {
    R invoke(P1 n);
}

private void reorderOddEven_2(int[] pData, int length) {
    reorder(pData, length, new IsEvenFunction());
}

private void reorder(int[] pData, int length, Function<Integer, Boolean> function) {
    if (pData == null || length == 0) {
        return;
    }

    int lo = 0, hi = length - 1;

    while (lo < hi) {
        // 向后移动pBegin，直到它指向偶数
        while (lo < hi && !function.invoke(pData[lo])) {
            lo++;
        }

        // 向前移动pEnd，直到它指向奇数
        while (lo < hi && function.invoke(pData[hi])) {
            hi--;
        }

        if (lo < hi) {
            int temp = pData[lo];
            pData[lo] = pData[hi];
            pData[hi] = temp;
        }
    }
}

private class IsEvenFunction implements Function<Integer, Boolean> {
    @Override
    public Boolean invoke(Integer n) {
        return (n & 1) == 0;
    }
}

在上面的代码中，方法根据function的实现把数组分成两部分。如果把问题改成数组中的负数移到非负数的前面，或者把能被3整除的数移到不能被3整除的数前面，都只需要定义新的函数来确定分组的标准，而方法不需要进行任何修改。也就是说，解耦的好处就是提高了代码的重用性，为功能扩展提供了便利。

2. 代码的鲁棒性¶

鲁棒是英文 Robust 的音译，也翻译成健壮性。所谓鲁棒性是指程序能够判断输入是否合乎规范要求，并对不符合要求的输入予以合理的处理。
容错性是鲁棒性的一个重要体现。
提高代码的鲁棒性的有效途径是进行防御性编程。防御性编程是一种编程习惯，是指预见在什么地方可能会出现问题，并为这些可能出现的问题制定处理方式。
在面试时，最简单也最实用的防御性编程就是在函数入口添加代码以验证用户输入是否符合要求。
当然，并不是所有与鲁棒性相关的问题都只是检查输入的参数那么简单。

2.1 (22)链表中倒数第k个结点¶

输入一个链表，输出该链表中倒数第k个结点。为了符合大多数人的习惯，本题从1开始计数，即链表的尾结点是倒数第1个结点。例如一个链表有6个结点，从头结点开始它们的值依次是1、2、3、4、5、6。这个链表的倒数第3个结点是值为4的结点。

该题同LC-19-Remove Nth Node From End of List

代码Copy如下：

private ListNode findKthToTail(ListNode pListHead, int k) {
    if (pListHead == null || k <= 0) {
        return null;
    }

    ListNode p = pListHead;
    int i = 1;
    while (i < k && p != null) {
        p = p.next;
        i++;
    }

    if (p == null) {
        return null;
    }

    ListNode q = pListHead;
    while (p.next != null) {
        p = p.next;
        q = q.next;
    }

    return q;
}

2.2 (23)链表中环的入口结点¶

一个链表中包含环，如何找出环的入口结点？例如，在图3.8的链表中，环的入口结点是结点3。

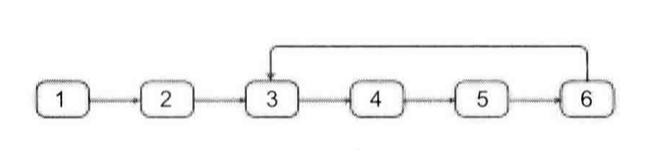
节点3是链表中环的入口节点

解决这个问题的第一步是如何确定一个链表中包含环。第二步是如何找到环的入口。

解法步骤如下：

找出环中任意一个节点；
得到环中节点的数目；
找到环的入口节点。

private ListNode entryNodeOfLoop(ListNode head) {
    ListNode meetingNode = meetingNode(head);
    if (meetingNode == null) {
        return null;
    }

    // 计算环中节点个数
    int nodesInLoop = 1;
    ListNode node1 = meetingNode;
    while (node1.next != meetingNode) {
        nodesInLoop++;
        node1 = node1.next;
    }

    // 将node1从头开始移动nodesInLoop次
    node1 = head;
    for (int i = 0; i < nodesInLoop; i++) {
        node1 = node1.next;
    }

    // 将node1、node2同时移动
    ListNode node2 = head;
    while (node1 != node2) {
        node1 = node1.next;
        node2 = node2.next;
    }

    return node1;
}

private ListNode meetingNode(ListNode head) {
    if (head == null) {
        return null;
    }

    ListNode slow = head.next;
    if (slow == null) {
        return null;
    }

    ListNode fast = slow.next;
    while (fast != null && slow != null) {
        if (fast == slow) {
            return fast;
        }

        slow = slow.next;

        fast = fast.next;
        if (fast != null) {
            fast = fast.next;
        }
    }

    return null;
}

2.3 (24)反转链表¶

定义一个函数，输入一个链表的头结点，反转该链表并输出反转后链表的头结点。

private ListNode reverseList(ListNode head) {
    if (head == null || head.next == null) {
        return head;
    }

    ListNode p = head, q = p.next;
    head.next = null;

    while (q != null) {
        p = q.next;
        q.next = head;
        head = q;
        q = p;
    }

    return head;
}

此题注意需要用以下几类测试用例对代码进行功能测试：

输入的链表头指针是null
输入的链表只有一个节点
输入的链表有多个节点

本题扩展

用递归实现同样的反转链表的功能。

private ListNode reverseList(ListNode head) {
    if (head == null || head.next == null) {
        return head;
    }

    ListNode next = head.next;
    head.next = null;
    ListNode reversed = reverseList(next);
    next.next = head;

    return reversed;
}

2.4 (25)合并两个排序的链表¶

输入两个递增排序的链表，合并这两个链表并使新链表中的结点仍然是按照递增排序的。例如输入图中的链表1和链表2，则合并之后的升序链表如链表3所示。

合并两个链表排序的过程

此题同LC-21-Merge Two Sorted Lists。

注意操作列表最好不要直接操作入参列表，所以合并的时候会创建一些节点。

代码Copy如下：

class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        ListNode result = new ListNode(0), p = l1, q = l2, m = result;

        while (p != null || q != null) {
            if (p == null) {
                m.next = q;
                return result.next;
            }
            if (q == null) {
                m.next = p;
                return result.next;
            }
            if (p.val < q.val) {
                m.next = new ListNode(p.val);
                p = p.next;
            } else {
                m.next = new ListNode(q.val);
                q = q.next;
            }
            m = m.next;
        }

        return result.next;
    }
}

2.5 (26)树的子结构¶

输入两棵二叉树A和B，判断B是不是A的子结构。

例如图中的两颗二叉树，由于A中有一部分子树的结构和B是一样的，因此B是A的子结构。

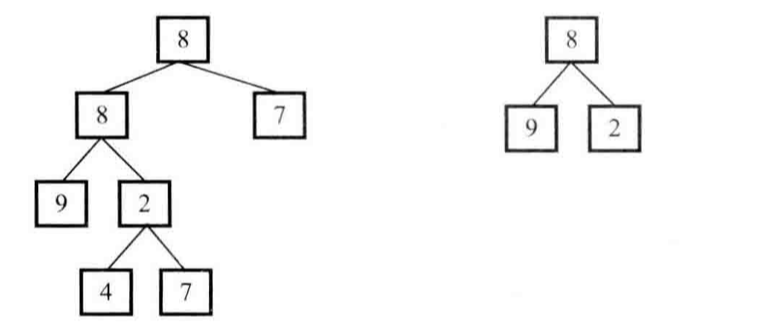
两颗二叉树A和B，右边的树B是左边的树A的子结构

要查找树A中是否存在和树B结构一样的子树，我们可以分为两步：

第一步，在树A中找到和树B的根节点的值一样的节点R
第二步，判断树A中以R为根节点的子树是不是包含和树B一样的结构

private boolean hasSubtree(BinaryTreeNode root1, BinaryTreeNode root2) {
    boolean result = false;

    if (root1 != null && root2 != null) {
        result = doesTree1HasTree2(root1, root2);
        if (!result) {
            result = hasSubtree(root1.left, root2);
        }
        if (!result) {
            result = hasSubtree(root1.right, root2);
        }
    }

    return result;
}

private boolean doesTree1HasTree2(BinaryTreeNode root1, BinaryTreeNode root2) {
    if (root2 == null) {
        return true;
    }

    if (root1 == null) {
        return false;
    }

    if (root1.value != root2.value) {
        return false;
    }

    return doesTree1HasTree2(root1.left, root2.left) &&
            doesTree1HasTree2(root1.right, root2.right);
}

Tip

与二叉树相关的代码有大量的指针操作，在每次使用指针的时候，我们都要问自己这个指针有没有可能是null，如果是null则该怎么处理。

高质量的代码

1. 代码的完整性¶

1.1 (16)数值的整数次方¶

1.2 (17)打印1到最大的n位数¶

1.3 (18)删除链表的节点¶

1.3.1 在O(1)时间删除链表结点¶

1.3.2 删除链表中重复的结点¶

1.4 (19)正则表达式匹配¶

1.5 (20)表示数值的字符串¶

1.6 (21)调整数组顺序使奇数位于偶数前面¶

2. 代码的鲁棒性¶

2.1 (22)链表中倒数第k个结点¶

2.2 (23)链表中环的入口结点¶

2.3 (24)反转链表¶

2.4 (25)合并两个排序的链表¶

2.5 (26)树的子结构¶

评论