数据结构、算法和数据操作
1. 数组¶
1.1 (3)数组中重复的数字¶
1.1.1 找出数组中重复的数字¶
在一个长度为n的数组里的所有数字都在0到n-1的范围内。数组中某些数字是重复的,但不知道有几个数字重复了,也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。例如,如果输入长度为7的数组{2, 3, 1, 0, 2, 5, 3},那么对应的输出是重复的数字2或者3。
解法一:先排序,后遍历
排序后找到重复的数字是非常容易的事情,只需要从头到尾扫描排序后的数组就可以了。
排序一个长度为n的数组需要O(nlogn)的时间
解法二:哈希表
从头到尾扫描,每扫到一个数字,可以用O(1)的时间判断哈希表中是否已经包含了该数字。如果没有包含,就把它加入哈希表。否则,就找到了重复数字。
其时间复杂度为O(n),空间复杂度也为O(n)
解法三:利用数组的特点
我们注意到数组中的数字都在0~n-1的范围内。如果数组中没有重复元素,那么数组排序后数字i将会出现在下标为i的位置。如果有重复的元素,那么有些位置可能存在多个数字,同时有些位置可能没有数字。
我们从头到尾遍历数组。当扫描到下标为i的数字时,首先比较这个数字(m)是不是i。如果是,则接着扫描下一个数字;如果不是,拿它和第m个数字进行比较。如果它和第m个数字相等,就找到了一个重复的数字(该数字在下标i和m的位置都出现了)。如果它和第m个数字不相等,就把第i个数字和第m个数字交换,把m放到属于它的位置。接下来再重复这个比较、交换的过程。
private int duplicate(int[] numbers, int length) {
if (numbers == null || length == 0) {
return -1;
}
for (int i = 0; i < length; i++) {
if (numbers[i] < 0 || numbers[i] >= length) {
return -1;
}
}
for (int i = 0; i < length; i++) {
while (numbers[i] != i) {
if (numbers[i] == numbers[numbers[i]]) {
return numbers[i];
}
// swap
int t = numbers[i];
numbers[i] = numbers[t];
numbers[t] = t;
}
}
return -1;
}
此题思想和LC—41—First Missing Positive思想类似。
1.1.2 不修改数组找出重复的数字¶
在一个长度为n+1的数组里的所有数字都在1到n的范围内,所以数组中至少有一个数字是重复的。请找出数组中任意一个重复的数字,但不能修改输入的数组。例如,如果输入长度为8的数组{2, 3, 5, 4, 3, 2, 6, 7},那么对应的输出是重复的数字2或者3。
解法一:复制数组时排序
我们可以创建一个长度为n+1的辅助数组,然后逐一辅助原数组中的每个数字。在复制时,如果原数组中被复制的数字是m,则把它复制到辅助数组中下标为m的位置。这样就容易发现哪个数字是重复的。
该方法时间复杂度为O(1),空间复杂度为O(n)。
解法二:利用题设
在一个长度为n+1的数组里的所有数字都在1到n的范围内,所以数组中至少有一个数字是重复的。
由于所有的数字都在1~n的范围内,所以我们可以利用二分查找,在查找时统计一下某个区间里数字的数目。
我们把1~n的数字从中间的数字m分为两部分,前面一半为1~m,后面一半为m+1~n。如果1~m的数字出现的次数超过m,那么这一半的区间里一定包含重复的数字;否则另一半区间里一定包含重复的数字。我们可以继续把包含重复数字的区间一分为二,直到找到一个重复的数字。
该方法由于二分查找的特点,countRange方法会被调用O(logn)次,每次需要O(n)的时间,因此总时间复杂度是O(nlogn),空间复杂度为O(1)。
// 题设:n+1的数组里的所有数字都在1到n的范围内
// 可以换成好理解的:n的数组里的所有数字都在1到n-1的范围内
private int duplicate(int[] numbers, int length) {
if (numbers == null || length == 0) {
return -1;
}
for (int i = 0; i < length; i++) {
if (numbers[i] < 0 || numbers[i] >= length) {
return -1;
}
}
// start、end是需要统计的数字的上下限
int start = 1;
int end = length - 1;
int mid = 0;
while (end >= start) {
mid = ((end - start) >> 1) + start;
int count = countRange(numbers, start, mid);
if (start == end) {
if (count > 1) {
// 找到了,当前指向的值就是重复数字
return start;
} else {
// 否则,没有重复数字
break;
}
}
// 如果区间内的出现的数字个数大于区间的长度,说明这个区间出现了重复数字
if (count > (mid - start + 1)) {
// 此时重复的值可能就是mid,所以end=mid
end = mid;
} else {
// 如果该区间没有重复数字,那么mid肯定也不是,所以跳过mid
start = mid + 1;
}
}
return -1;
}
private int countRange(int[] numbers, int start, int end) {
int count = 0;
for (int i = 0; i < numbers.length; i++) {
if (numbers[i] >= start && numbers[i] <= end) {
count++;
}
}
return count;
}
1.2 (4)二维数组中的查找¶
在一个二维数组中,每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
下面就是一个示例数组。在其中查找7返回true,查找5返回false。
我们利用每行每列都是递增的规律,可以整行、整列地缩减查找范围。
首选选取数组右上角的数字。如果数字等于要查找的数字,则查找过程结束;如果该数字大于要查找的数字,说明要查找的数字位于该列左边,所以剔除这个数字所在的列;如果该数字小于要查找的数字,说明要查找的数字位于改行下方,所以剔除这个数字所在的行。这样每一步都可以缩小查找的方位,直到找到数字或查找结束。
boolean find(int[][] matrix, int rows, int columns, int number) {
if (matrix == null || rows == 0 || columns == 0) {
return false;
}
int row = 0;
int col = columns - 1;
while (row < rows && col >= 0) {
if (matrix[row][col] == number) {
return true;
} else if (matrix[row][col] > number) {
col--;
} else {
row++;
}
}
return false;
}
在上面的代码中,我们选取的右上角的数字。同样,我们也可以选择左下角的数字,也可以逐步减小查找范围。其他两个角因为是最小值、最大值,无法逐步减小查找范围。
int row = rows - 1;
int col = 0;
while (col < columns && row >= 0) {
if (matrix[row][col] == number) {
return true;
} else if (matrix[row][col] > number) {
row--;
} else {
col++;
}
}
2. 字符串¶
2.1 (5)替换空格¶
请实现一个函数,把字符串中的每个空格替换成"%20"。例如输入“We are happy.”,则输出“We%20are%20happy.”。
解法一:顺序查找空格,找到后插入%20
假设字符串的长度为n。对于每个空格字符,需要移动和面O(n)个字符,对于含有O(n)个空格字符的字符串而言,总的时间效率是O(n^2)。
解法二:计算空格个数,从后往前替换空格
我们可以先遍历一次字符串,统计出空格的总数,由此可以计算出新串的总长度。然后从字符串的后面(或前面)开始复制和替换,方向没有多少区别。
String replaceBlank(String str) {
if (str == null || "".equals(str)) {
return str;
}
// 统计空格的个数
int spaceCount = 0;
for (int i = 0; i < str.length(); i++) {
if (str.charAt(i) == ' ') {
spaceCount++;
}
}
// 如果不包含空格,就可以直接返回原来的字符串
if (spaceCount == 0) {
return str;
}
// 申请新串,准备复制
final int newStrLength = str.length() + spaceCount * 2;
char[] result = new char[newStrLength];
int index = newStrLength - 1;
// 在原来的串上从后往前遍历
for (int i = str.length() - 1; i >= 0; i--) {
if (str.charAt(i) == ' ') {
// 遇到一个空格,则在新串上填上%20
result[index--] = '0';
result[index--] = '2';
result[index--] = '%';
} else {
// 复制原来的字符
result[index--] = str.charAt(i);
}
}
return new String(result);
}
也可以在Java中直接使用StringBuilder的特点解决此问题:
String replaceBlank(String str) {
if (str == null || "".equals(str)) {
return str;
}
StringBuilder result = new StringBuilder();
for (int i = 0; i < str.length(); i++) {
char ch = str.charAt(i);
if (ch == ' ') {
result.append("%20");
} else {
result.append(ch);
}
}
return result.toString();
}
相关题目
有两个排序的数组A1和A2,内存在A1的末尾有足够多的剩余空间容纳A2。请实现一个函数,把A2中的所有数字插入A1中,并且所有的数字是排序的。
和前面的例题一样,很多人首先想到的办法是在A1中从头到尾复制数字,但这样就会出现多次复制一个数字的情况。更好的的方法是 从尾到头 比较A1和A2中的数字,并把较大的数字复制到A1中的合适位置。
举一反三
在合并两个数组时,如果从前往后复制每个数字需要重复移动数字多次,那么我们可以考虑从后往前复制,这样就能减少移动的次数,从而提高效率。
3. 链表¶
3.1 (6)从尾到头打印链表¶
输入一个链表的头结点,从尾到头反过来打印出每个结点的值。
通常打印只是一个只读操作,我们不希望打印时修改内容。
此题如果想把链表中链接节点的指针反转过来,改变链表的方向,这样就太蠢了,而且也会改变原来链表的结构。
我们可以想到遍历时使用Stack保存节点的值,然后全部出栈就可以了。
解法一:利用栈
private void printListReversingly1(ListNode pHead) {
ListNode p = pHead;
Stack<Integer> stack = new Stack<>();
while (p != null) {
stack.push(p.value);
p = p.next;
}
while (!stack.isEmpty()) {
System.out.print(stack.pop() + "\t");
}
}
既然想到了用栈实现,而递归本质上就是一个栈结构,所以我们也可以利用递归实现。
要反过来输出链表,我们每访问一个节点时,先递归输出它后面的节点,再输出该节点自身,这样就实现了目的。
解法二:递归
private void printListReversingly2(ListNode pHead) {
if (pHead != null) {
printListReversingly1(pHead.next);
System.out.print(pHead.value + "\t");
}
}
上面的代码看起来很简洁,但 当链表非常长的时候,就会导致函数调用的层级很深,从而导致函数调用栈溢出 。显然用栈基于循环实现的代码鲁棒性要好一点。
4. 树¶
树的逻辑结构很简单:除根节点之外的每个节点只有一个父节点,根节点没有父节点;除叶节点之外所有节点都有一个或多个子节点,叶节点没有子节点。父节点与子节点之间用指针链接。
我们常提到的树是二叉树,通常二叉树有如下几种遍历方式。
- 前序遍历:根左右,即先访问根节点,再访问左子节点,最后访问右子节点。
图中二叉树的前序遍历的顺序是,10、6、4、8、14、12、16 - 中序遍历:左根右,即先访问左子节点,再访问根节点,最后访问右子节点。
图中二叉树的中序遍历的顺序是,4、6、8、10、12、14、16 -
后序遍历:左右根,即先访问左子节点,再访问右子节点,最后访问根节点。
图中二叉树的中序遍历的顺序是,4、8、6、12、16、14、10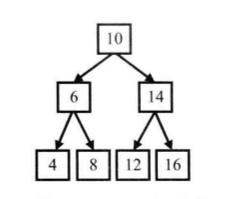
这三种遍历方式都有递归和循环2种实现方式,每种遍历的递归实现都比循环实现要简洁很多。我们应该对这3中遍历的6种实现方法都了如指掌。 -
宽度优先遍历:先访问树的第一层节点,再访问树的第二层节点……一直到访问到最下面一层节点。在同一层节点中,以从左到右的顺序依次访问。我们可以对包括二叉树在内的所有树进行宽度优先遍历。
图中二叉树的宽度优先遍历的顺序是:10、6、14、4、8、12、16
树的遍历算法¶
/**
* 前序遍历递归算法
*/
private static void preorderRecursive(BinaryTreeNode node) {
if (node != null) {
System.out.print(" " + node.value);
preorderRecursive(node.left);
preorderRecursive(node.right);
}
}
/**
* 前序遍历循环算法
* 从根节点开始,每访问一节点时,先访问左子树,同时若右子树存在,则将右子树进栈
*/
private static void preorderIterative(BinaryTreeNode node) {
if (node == null) {
return;
}
Stack<BinaryTreeNode> stack = new Stack<>();
BinaryTreeNode p;
// 根节点进栈
stack.push(node);
while (!stack.isEmpty()) {
// 开始访问当前栈顶的元素
p = stack.pop();
while (p != null) {
// 访问当前栈顶的元素
System.out.print(" " + p.value);
// 若右节点存在,则将右子树进栈
if (p.right != null) {
stack.push(p.right);
}
// 继续沿着左子树访问
p = p.left;
}
}
}
/**
* 中序遍历递归算法
*/
private static void inorderRecursive(BinaryTreeNode node) {
if (node != null) {
inorderRecursive(node.left);
System.out.print(" " + node.value);
inorderRecursive(node.right);
}
}
/**
* 中序遍历循环算法
* 从根节点开始,沿着左子树找到该子树在中序下的第一节点(同时保存每个节点到栈内),访问该节点
* 然后访问该节点的右子树
*/
private static void inorderIterative(BinaryTreeNode node) {
if (node == null) {
return;
}
Stack<BinaryTreeNode> stack = new Stack<>();
BinaryTreeNode p;
// 根节点进栈
stack.push(node);
while (!stack.isEmpty()) {
// 开始访问栈顶的元素
p = stack.peek();
// 若左子树存在,一直将左子树压进栈
while (p != null) {
stack.push(p.left);
p = stack.peek();
}
// 弹出栈顶的空元素
stack.pop();
if (!stack.isEmpty()) {
// 叶节点或没有左子树的节点
p = stack.pop();
// 访问当前栈顶的元素
System.out.print(" " + p.value);
// 将右子树进栈,在循环的开始就能处理右子树了
stack.push(p.right);
}
}
}
/**
* 后序遍历递归算法
*/
private static void postorderRecursive(BinaryTreeNode node) {
if (node != null) {
postorderRecursive(node.left);
postorderRecursive(node.right);
System.out.print(" " + node.value);
}
}
private static class NodeWrapper {
public BinaryTreeNode node;
/**
* false表示左子树压入的
* true表示右子树压入的
*/
public boolean tag;
}
/**
* 后序遍历循环算法
* 对于一个节点是否能够访问,要看它的左右子树是否遍历完
* 首先从根节点开始,沿着左子树开始遍历,将途中所有节点全部标记并压入栈中
* 然后取栈顶元素,如果能够访问右子树,则沿着右子树开始遍历,将途中所有节点全部标记并压入栈中
* 若左右都访问完毕,则访问自身这个节点
*/
private static void postorderIterative(BinaryTreeNode node) {
if (node == null) {
return;
}
Stack<NodeWrapper> stack = new Stack<>();
BinaryTreeNode p = node;
NodeWrapper wrapper;
while (p != null || !stack.isEmpty()) {
// 沿着左子树开始遍历,将途中所有节点全部标记并压入栈中
while (p != null) {
wrapper = new NodeWrapper();
wrapper.node = p;
wrapper.tag = false;
stack.push(wrapper);
p = p.left;
}
// 取栈顶元素
wrapper = stack.pop();
p = wrapper.node;
boolean find = wrapper.tag;
if (!find) {
// 能够访问右子树,则沿着右子树开始遍历,将途中所有节点全部标记并压入栈中
wrapper = new NodeWrapper();
wrapper.node = p;
wrapper.tag = true;
stack.push(wrapper);
p = p.right;
} else {
// 左右都访问完毕,则访问自身这个节点
System.out.print(" " + p.value);
p = null;
}
}
}
/**
* 层序遍历算法
*/
private static void levelIterative(BinaryTreeNode node) {
Queue<BinaryTreeNode> queue = new LinkedList<>();
queue.offer(node);
while (!queue.isEmpty()) {
node = queue.poll();
System.out.print(" " + node.value);
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
}
树的其他概念¶
若设二叉树的深度为h,除第h层外,其它各层 (1~h-1) 的结点数都达到最大个数,第h层所有的结点都连续集中在最左边,这就是 完全二叉树。
二叉搜索树、二叉查找树、二叉排序树 是一个概念:左子节点总是小于或者等于根节点,而右子节点总是大于或者等于根节点。
平衡二叉树AVL 是一颗二叉搜索树,每个节点的左右子树的高度差的绝对值(平衡因子)最多为1。
二叉树有很多特例,二叉搜索树 就是其中之一。
在二叉搜索树中,左子节点总是小于或者等于根节点,而右子节点总是大于或者等于根节点。上面练习树的遍历算法的二叉树就是一颗二叉搜索树。我们平均在O(logn)的时间内根据数值在二叉搜索树中找到一个节点。
二叉树的另外两个特例是 堆 和 红黑树。
-
堆分为 最大堆 和 最小堆。在最大堆中根节点的值最大,在最小堆中根节点的值最小。有很多需要快速找到最大值或者最小值的问题都可以用堆解决。
最小堆、最大堆在Java中可以这样实现: -
关于红黑树,维基百科说的非常好:红黑树
红黑树 是一种近似平衡的二叉查找树,它把树中的节点定义为红、黑两种颜色,并通过规则确保从根节点到叶节点的最长路径的长度不超过最短路径的两倍。
具体来说,红黑树是满足如下条件的二叉查找树:- 每个节点要么是红色,要么是黑色。
- 根节点必须是黑色
- 每个叶节点(在红黑树中指树尾端的null节点)都是黑色
- 红色节点不能连续(也即是,红色节点的孩子和父亲都不能是红色)。
- 对于每个节点,从该点至null(树尾端)的任何路径,都含有相同个数的黑色节点。
一个红黑树例子如下:

这些约束确保了红黑树的关键特性:从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这个树大致上是平衡的。 因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例,这个在高度上的理论上限允许红黑树在最坏情况下都是高效的,而不同于普通的二叉查找树。
要知道为什么这些性质确保了这个结果,注意到性质4导致了路径不能有两个毗连的红色节点就足够了。最短的可能路径都是黑色节点,最长的可能路径有交替的红色和黑色节点。因为根据性质5所有最长的路径都有相同数目的黑色节点,这就表明了没有路径能多于任何其他路径的两倍长。
在树的结构发生改变时(插入或者删除操作),往往会破坏上述条件4或条件5,需要通过调整使得查找树重新满足红黑树的条件。
调整可以分为两类:一类是颜色调整,即改变某个节点的颜色;另一类是结构调整,集改变检索树的结构关系。结构调整过程包含两个基本操作:左旋(Rotate Left),右旋(Rotate Right)。
Java中TreeMap底层通过红黑树来实现,这样插入删除都只有\(O(logn)\)的时间复杂度。
4.1 (7)重建二叉树¶
输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
例如输入前序遍历序列{1,2, 4, 7, 3, 5, 6, 8}和中序遍历序列{4, 7, 2, 1, 5, 3, 8, 6},则重建下图所示的二叉树并输出它的头结点。
此题同LC-105-Construct Binary Tree from Preorder and Inorder Traversal
Tip
前序+中序、后序+中序、层序+中序都可以重建二叉树,但是前序+后序不行。
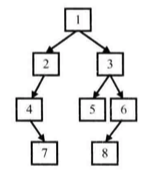
算法思路是先根据前序序列找到根节点,然后在中序序列中找到该节点,其左边的就是树的左子树,右边就是右子树。
private BinaryTreeNode construct(int[] preorder, int[] inorder, int length) throws Exception{
if (preorder == null || inorder == null || length <= 0) {
return null;
}
return constructCore(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1);
}
private BinaryTreeNode constructCore(
int[] preorder, int startPreorder, int endPreorder,
int[] inorder, int startInorder, int endInorder
) throws Exception {
// 如果发生了这种情况,说明前中序子序列为空,那么肯定就是空节点了
if (startInorder > endInorder || startPreorder > endPreorder) {
return null;
}
// startPreorder即为根节点
BinaryTreeNode root = new BinaryTreeNode(preorder[startPreorder]);
boolean find = false;
int i = startInorder;
for (; i <= endInorder; i++) {
if (inorder[i] == root.value) {
find = true;
// 由于在中序序列中i是根节点,所以i-startInorder的长度就是左子树的长度
// 因此重建左子树时,左子树的前序序列范围就是startPreorder+1至startPreorder+1 + i-startInorder - 1 = startPreorder + i - startInorder
// 左子树的中序序列范围就是startInorder至i - 1,没有什么好说的
// 重建右子树时类似
root.left = constructCore(
preorder, startPreorder + 1, startPreorder + i - startInorder,
inorder, startInorder, i - 1);
root.right = constructCore(
preorder, startPreorder + i - startInorder + 1, endPreorder,
inorder, i + 1, endInorder);
}
}
// 最后,如果根节点在中序序列中没有找到,那么肯定是无效的输入了
if (!find) {
throw new Exception("invalid input");
}
return root;
}
4.2 (8)二叉树的下一个节点¶
给定一棵二叉树和其中的一个结点,如何找出中序遍历顺序的下一个结点?树中的结点除了有两个分别指向左右子结点的指针以外,还有一个指向父结点的指针。
下图中二叉树的中序遍历序列是{d, b, h, e, i, a, f, c, g}。
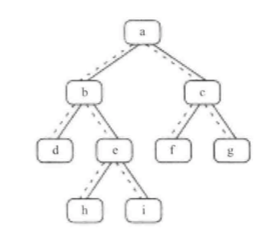
我们以上面这颗树为例分析如何找出二叉树的下一个节点。
- 根,如果一个节点有右子树:那么它的下一个节点就是它的右子树中的最左子节点。也就是说,从右子节点出发一直沿着指向左子节点的指针,我们就能找到它的下一个节点。
- 左,如果一个节点没有右子树,同时节点是它父节点的左子节点,那么它的父节点就是要找的下一个节点。
- 右,如果一个节点没有右子树,同时节点是它父节点的右子节点:我们需要沿着父节点一直向上,直到找到一个是它父节点的左子节点的节点。这个父节点就是我们要找的下一个节点。
private ParentBinaryTreeNode getNext(ParentBinaryTreeNode node){
if (node == null) {
return null;
}
ParentBinaryTreeNode next = null;
if (node.right != null) {
// 情况1 从右子节点出发一直沿着指向左子节点的指针
next = node.right;
while (next.left != null) {
next = next.left;
}
return next;
} else if (node.parent != null) {
// 情况2、3可以理解为同一种 2是3的一般情况
next = node;
// 沿着父节点一直向上,直到找到一个节点,它是父节点的左子节点
// 即如果这个节点是父节点的右节点,那么继续寻找
while (next.parent != null && next == next.parent.right) {
next = next.parent;
}
// 最后这个父节点就是我们要找的下一个节点
return next.parent;
}
return next;
}
5. 栈和队列¶
栈的特点是后进先出,通常栈是一个不考虑排序的数据结构,我们需要O(n)时间才能找到栈中最大或者最小的元素。如果想要在O(1)时间内得到栈的最大值或最小值,则需要对栈做特殊的设计,详见(30)题“包含min函数的栈”。
队列的特点是先进先出。
栈和队列虽然是特点针锋相对的两个数据结构,但有意思的是他们却相互联系。
栈的常用操作为:
isEmptypeekpoppush
队列的常用操作为:
isEmptypeekpolloffer
5.1 (9)用两个栈实现队列¶
用两个栈实现一个队列。队列的声明如下,请实现它的两个函数appendTail和deleteHead,分别完成在队列尾部插入结点和在队列头部删除结点的功能。
class JQueue<T> {
private Stack<T> stack1 = new Stack<>();
private Stack<T> stack2 = new Stack<>();
public void appendTail(T element) {
stack1.push(element);
}
public T deleteHead() {
if (stack2.isEmpty()) {
while (!stack1.isEmpty()) {
stack2.push(stack1.pop());
}
}
if (stack2.isEmpty()) {
return null;
}
return stack2.pop();
}
}
插入元素的时候直接插入stack1即可。
在删除队列的头部的时候,如果stack2为空,那么把stack1的pop依次push进stack2。这样操作后stack2中最上面就是最先进队列的,也就是我们要求的。
相关题目
用两个队列实现一个栈。
/**
* 相关题目
* 用两个队列实现一个栈。
*/
class JStack<T> extends Stack<T>{
private Queue<T> queue1 = new LinkedList<>();
private Queue<T> queue2 = new LinkedList<>();
@Override
public T push(T item) {
queue1.offer(item);
return item;
}
@Override
public synchronized T pop() {
if (queue1.isEmpty()) {
throw new EmptyStackException();
}
while (queue1.size() > 1) {
queue2.offer(queue1.poll());
}
T item = queue1.poll();
Queue<T> tmp = queue1;
queue1 = queue2;
queue2 = tmp;
return item;
}
public static void main(String[] args) {
Stack<Integer> stack = new JStack<>();
stack.push(1);
System.out.println(stack.pop());
stack.push(2);
stack.push(3);
System.out.println(stack.pop());
stack.push(4);
System.out.println(stack.pop());
System.out.println(stack.pop());
// 输出 1 3 4 2
}
}
6. 算法和数据操作¶
很多算法都可以用递归和循环两种不同的方式实现。通常基于递归的实现方式代码会比较简洁,但性能不如基于循环的实现方式。
通常排序和查找时算法的重点。我们应该重点掌握二分查找、归并排序和快速排序,能做到随时正确、完整地写出这些代码。
如果要求在二维数组上搜索路径,那么我们可以尝试用回溯法。通常回溯法很适合用递归的代码实现。只有限定不能用递归实现的时候,我们再考虑用栈来模拟递归的过程。
如果要求的是某个问题的最优解,而且该问题可以分为多个子问题,那么我们可以尝试用动态规划。在用自上而下的递归思路去分析动态规划问题的时候,我们就会发现子问题之间存在重叠的更小的子问题。为了避免不必要的重复计算,我们用自下而上的循环代码来实现,也就是把子问题的最优解先计算出来并用数组保存下来,接下来基于子问题的解计算大问题的解。 如果在分解子问题的时候存在某个特殊的选择,如果采用这个特殊的选择将一定得到最优解,那么这意味着可能适用于贪婪算法。
位运算可以看成一类特殊的算法,它是把数字表示成二进制之后对0和1的操作。它只有与、或、异或、左移、右移5种位运算。
6.1 递归和循环¶
如果我们需要重复地多次计算相同的问题,则通常可以选择用递归或者循环两种不同的方法。通常递归的代码会比较简洁。
虽然递归很简洁,但它同时也有显著的缺点。递归是函数调用自身,而函数调用时有时间和空间的消耗的,所以递归实现的效率不如循环。
另外,递归中有可能很多计算都是重复的,从而对性能带来很大的负面影响。例如第10题“斐波那契数列”和第60题“n个骰子的点数”中,我们会分析递归和循环的性能区别。
通常应用动态规划解决问题时我们都是用递归的思路分析问题,但由于递归分解的子问题中存在大量的重复,因此我们总是采用自下而上的循环来实现代码。例如第14题“剪绳子”、第47题”礼物的最大价值”和第48题”最长不含重复数字的子字符串”中我们会详细讨论如何用递归分析问题并基于循环写代码。
除效率之外,递归还有可能引起更严重的问题:调用栈溢出。
6.1.1 (10)斐波那契数列¶
写一个函数,输入n,求斐波那契(Fibonacci)数列的第n项。
解法一:递归
private long Fibonacci_Solution1(int n) {
if (n == 0)
return 0;
else if (n == 1)
return 1;
else
return Fibonacci_Solution1(n - 1) + Fibonacci_Solution1(n - 2);
}
这种解法有很严重的效率问题。我们以求解f(10)为例,可以得到下面的调用图。
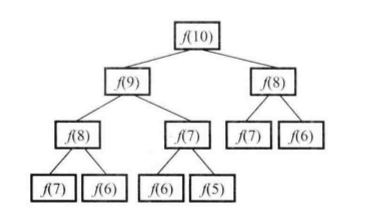
我们不难发现,在这棵树中有很多节点都是重复的,而且重复的节点数会随着n的增大而急剧增加。
该算法时间复杂度是O(2^n)
解法二:循环
private long Fibonacci_Solution2(int n) {
int[] results = {0, 1};
if (n < 2) {
return results[n];
}
int a = results[0];
int b = results[1];
int result = 0;
for (int i = 2; i <= n; i++) {
result = a + b;
a = b;
b = result;
}
return result;
}
该算法时间复杂度是O(n)
解法三:利用数学公式
利用上面的公式,我们只需要求得矩阵\(\begin{bmatrix}1 & 1 \\ 1 & 0\end{bmatrix}^{n-1}\)即可得到\(f(n)\)。如果只是简单地从0开始循环,n次方仍然需要n次运算,其时间复杂度还是\(O(n)\),并不比前面的快。所以我们需要利用乘方的如下性质:
用上面的公式可以看出,我们想求\(n\)次方,就要先求\(n/2\)次方,在把\(n/2\)次方平方一下即可。这可以用递归的思路实现。
private static class Matrix2By2 {
long m_00;
long m_01;
long m_10;
long m_11;
Matrix2By2(long m_00, long m_01, long m_10, long m_11) {
this.m_00 = m_00;
this.m_01 = m_01;
this.m_10 = m_10;
this.m_11 = m_11;
}
static Matrix2By2 matrixMultiply(Matrix2By2 matrix1, Matrix2By2 matrix2) {
return new Matrix2By2(
matrix1.m_00 * matrix2.m_00 + matrix1.m_01 * matrix2.m_10,
matrix1.m_00 * matrix2.m_01 + matrix1.m_01 * matrix2.m_11,
matrix1.m_10 * matrix2.m_00 + matrix1.m_11 * matrix2.m_10,
matrix1.m_10 * matrix2.m_01 + matrix1.m_11 * matrix2.m_11);
}
static Matrix2By2 MatrixPower(int n) {
Matrix2By2 matrix;
if (n == 1) {
matrix = new Matrix2By2(1, 1, 1, 0);
} else if (n % 2 == 0) {
matrix = MatrixPower(n / 2);
matrix = matrixMultiply(matrix, matrix);
} else { // n % 2 == 1
matrix = MatrixPower((n - 1) / 2);
matrix = matrixMultiply(matrix, matrix);
matrix = matrixMultiply(matrix, new Matrix2By2(1, 1, 1, 0));
}
return matrix;
}
}
private long Fibonacci_Solution3(int n) {
int[] results = {0, 1};
if (n < 2) {
return results[n];
}
Matrix2By2 matrix2By2 = Matrix2By2.MatrixPower(n - 1);
return matrix2By2.m_00;
}
该算法时间复杂度是\(O(logn)\),在第16题”数值的整数次方”中会讨论这种算法。
相关题目
青蛙跳台阶问题:一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个n级的台阶总共有多少种跳法。
相关题目
我们可以用2x1的小矩形横着或者竖着去覆盖更大的矩形。请问用8个2x1的小矩形无重叠地覆盖一个2x8的大矩形有多少种覆盖方法。
\(f(8)=f(7)+f(6)\)
上面两个题目都是斐波那契数列的例子。
6.2 查找和排序¶
查找和排序都是在程序设计中经常用到的算法。查找相对而言较为简单,不外乎顺序查找、二分查找、哈希表查找和二叉排序树查找。
小提示
如果要求在排序的数组或者部分排序的数组中查找一个数字或统计某个数字出现的次数,我们都可以尝试用二分查找算法。
哈希表和二叉排序树查找的重点在于考察对应的数据结构而不是算法。哈希表最主要的优点是能够在O(1)时间内查找某一元素,是效率最高的查找方式;但其缺点是需要额外的空间实现哈希表。例如第50题“第一个只出现一次的字符”就是利用哈希表的特性来实现高效查找的。
与二叉排序树查找算法对应的数据结构是二叉搜索树。具体例子为第33题“二叉搜索树的后序遍历序列”和第36题“二叉搜索树与双向链表”。
排序与查找要复杂一点。我们需要知道插入排序、冒泡排序、归并排序、快速排序等不同算法的优劣,能够从额外空间消耗、平均时间复杂度和最差时间复杂度等方面去比较它们的优缺点。特别注意的是我们需要写出快速排序的代码。
实现快速排序算法的关键在于先在数组中选择一个数字,接下来把数组中的数字分为两部分,比选择的数字小的数字移到数组左边,比选择的数字大的移到数组右边。接下来可以用递归的思路分别对每次选中的数字的左右两边排序
public class QuickSort {
private static int partition(int[] numbers, int lo, int hi) {
if (numbers == null || numbers.length == 0 || lo < 0 || hi >= numbers.length) {
throw new IllegalArgumentException("Invalid params");
}
int key = numbers[lo];
while (lo < hi) {
// 比选择的数字小的数字移到数组左边
while (numbers[hi] >= key && hi > lo) {
hi--;
}
numbers[lo] = numbers[hi];
// 比选择的数字大的移到数组右边
while (numbers[lo] <= key && hi > lo) {
lo++;
}
numbers[hi] = numbers[lo];
}
numbers[hi] = key;
return hi;
}
public static void sort(int[] numbers, int lo, int hi) {
if (lo >= hi) {
return;
}
int index = partition(numbers, lo, hi);
sort(numbers, lo, index - 1);
sort(numbers, index + 1, hi);
}
public static void main(String[] args) {
int[] numbers = {4, 3, 1, 5, 6, 10, 7, 6, 8};
sort(numbers, 0, numbers.length - 1);
for (int num : numbers) {
System.out.print(" " + num);
}
}
}
上面的partition除了可以用在快速排序中,还可以用来实现在长度为n的数组中查找第k大的数字,第39题“数组中出现次数超过一半的数字”和第40题“最小的k个数”都可以用这个函数来解决。
插入排序
public static void sort(Comparable[] a) {
// 将a[]升序排列
int N = a.length;
for (int i = 0; i < N; i++) {
for (int j = i; j > 0 && AbsSort.less(a[j], a[j-1]); j--) {
AbsSort.exch(a, j, j-1);
}
}
}
冒泡排序
public static void sort(Comparable[] a){
// 将a[]升序排列
int N = a.length;
for (int i = 0; i < N - 1; i++) {
for (int j = 0; j < N - i - 1; j++) {
if (AbsSort.less(a[j], a[j+1])) {
AbsSort.exch(a, j, j+1);
}
}
}
}
自顶向下归并排序
public class Merge extends AbsSort{
private static Comparable[] aux; // 归并所需的辅助数组
public static void sort(Comparable[] a) {
aux = new Comparable[a.length];
sort(a, 0, a.length - 1);
}
private static void sort(Comparable[] a, int lo, int hi) {
if (hi <= lo) return;
int mid = lo + (hi - lo)/2;
sort(a, lo, mid);
sort(a, mid+1, hi);
merge(a, lo, mid, hi);
}
/**
* 原地归并
*/
public static void merge(Comparable[] a, int lo, int mid, int hi) {
int i = lo, j = mid+1;
for (int k = lo; k <= hi; k++)
aux[k] = a[k];
for (int k = lo; k <= hi; k++) {
if (i > mid) a[k] = aux[j++];
else if (j > hi) a[k] = aux[i++];
else if (less(aux[j], aux[i])) a[k] = aux[j++];
else a[k] = aux[i++];
}
}
}
自底向上的归并排序
public class MergeBU extends AbsSort{
private static Comparable[] aux;
public static void sort(Comparable[] a) {
int N = a.length;
aux = new Comparable[N];
for (int sz = 1; sz < N; sz = sz+sz) // sz子数组大小
for (int lo = 0; lo < N-sz; lo += sz+sz) // lo:子数组索引
merge(a, lo, lo+sz-1, Math.min(lo+sz+sz-1, N-1));
}
/**
* 原地归并
*/
public static void merge(Comparable[] a, int lo, int mid, int hi) {
int i = lo, j = mid+1;
for (int k = lo; k <= hi; k++)
aux[k] = a[k];
for (int k = lo; k <= hi; k++) {
if (i > mid) a[k] = aux[j++];
else if (j > hi) a[k] = aux[i++];
else if (less(aux[j], aux[i])) a[k] = aux[j++];
else a[k] = aux[i++];
}
}
}
以下是常见排序算法的总结:
| 排序方法 | 时间复杂度(平均) | 时间复杂度(最坏) | 时间复杂度(最好) | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡排序 | \(O(n^2)\) | \(O(n^2)\) | \(O(n)\) | \(O(1)\) | 稳定 |
| 简单选择排序 | \(O(n^2)\) | \(O(n^2)\) | \(O(n^2)\) | \(O(1)\) | 不稳定 |
| 直接插入排序 | \(O(n^2)\) | \(O(n^2)\) | \(O(n)\) | \(O(1)\) | 稳定 |
| 希尔排序 | \(O(n^{4/3})\) | \(O(n^2)\) | \(O(n)\) | \(O(1)\) | 不稳定 |
| 堆排序 | \(O(nlog n)\) | \(O(nlog n)\) | \(O(nlog n)\) | \(O(1)\) | 不稳定 |
| 快速排序 | \(O(nlog n)\) | \(O(n^2)\) | \(O(nlog n)\) | \(O(log n)\) | 不稳定 |
| 归并排序 | \(O(nlog n)\) | \(O(nlog n)\) | \(O(nlog n)\) | \(O(n)\) | 稳定 |
6.2.1 (11)旋转数组的最小数字¶
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个递增排序的数组的一个旋转,输出旋转数组的最小元素。例如数组{3, 4, 5, 1, 2}为{1, 2, 3, 4, 5}的一个旋转,该数组的最小值为1。
本题与LC-81-Search in Rotated Sorted Array II比较类似;且前者要找具体的值,本题找最小值。但是具体思维可以借鉴,这样处理可以一般情况。
考虑到以下特殊情况:当下标为lo和hi的两个数字相同的情况,当lo,mid,hi对应的数字都相等时,上面的算法认为此时最小的数字位于中间数字的前面。这可不一定。比如数组{1, 0, 1, 1, 1}和数组{1, 1, 1, 0, 1}都是增序数列{0, 1, 1, 1, 1}的一个旋转数组。在这两个数组中最小数字为别位于左右半区。所以上面的算法一定会失败一种情况。因此,当lo,mid,hi对应的数字都相等时,我们必须采用顺序查找。
具体算法如下:
int min(int[] numbers) {
if (numbers == null) {
throw new IllegalArgumentException("Invalid params");
} else if (numbers.length == 1) {
return numbers[0];
}
int lo = 0;
int hi = numbers.length - 1;
while (lo < hi) {
int mid = (lo + hi) >> 1;
// 当lo,mid,hi对应的数字都相等时,采用顺序查找
if (numbers[lo] == numbers[mid] &&
numbers[mid] == numbers[hi]) {
return minInOrder(numbers, lo, hi);
}
if (numbers[mid] > numbers[hi]) {
// a[mid]>a[hi],说明最小值在右边,且肯定不会是a[mid],因为a[mid]>a[hi]>=min
lo = mid + 1;
} else {
// a[mid]<=a[hi],最小值可能是mid,所以不能漏掉
hi = mid;
}
}
return numbers[hi];
}
private int minInOrder(int[] numbers, int start, int end) {
int min = numbers[start];
for (int i = start + 1; i <= end; i++) {
if (numbers[i] < min) {
min = numbers[i];
return min;
}
}
return min;
}
6.3 回溯法¶
回溯法可以看成蛮力法的升级版,它从解决问题每一步的所有可能选项里系统地选择出一个可行的解决方案。回溯法非常适合由多个步骤组成的问题,并且每个步骤都有很多选项。当我们在某一步选择了其中一个选项时,就进入下一步,然后又面临新的选项。我们就这样重复选择,直至到达最终的状态。
用回溯法解决的问题的所有选项可以形象地用树状结构表示。在某一步有n个可能的选项,那么该步骤可以看成是树状结构中的一个节点,每个选项看成树中节点连接线,经过这些连接线到达该节点的n个子节点。树的叶节点对应着终结状态。如果在叶节点的状态满足题目的约束条件,那么我们找到了一个可行的解决方案。
如果在叶节点的状态不满足约束条件,那么只好回溯到它的上一个节点在尝试其他的选项。如果上一个节点所有可能的选项都已经试过,并且不能到达满足约束条件的终结状态,则再次回溯到上一个节点。如果所有节点的所有选项都已经尝试过仍然不能到达满足约束条件的终结状态,则该问题无解。
通常回溯法适合用递归实现代码。当我们到达某一个节点时,尝试所有可能的选项并在满足条件的前提下递归地抵达下一个节点。
6.3.1 (12)矩阵中的路径¶
请设计一个函数,用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中任意一格开始,每一步可以在矩阵中向左、右、上、下移动一格。如果一条路径经过了矩阵的某一格,那么该路径不能再次进入该格子。例如在下面的3×4的矩阵中包含一条字符串“bfce”的路径(路径中的字母用下划线标出)。但矩阵中不包含字符串“abfb”的路径,因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后,路径不能再次进入这个格子。
这是一个可以用回溯法解决的典型题。首先,在矩阵中任选一个格子ch作为路径的起点。如果路径上第i个字符刚好是ch,那么到相邻的格子寻找路径上的第i+1个字符。除矩阵边界上的格子之外,其他格子都有4个相邻的格子。重复这个过程,直到路径上的所有字符都在矩阵中找到相应的位置。
由于回溯法的递归特性,路径可以看成一个栈。当在矩阵中定位了路径中前n个字符的位置之后,在与第n个字符对应的格子的周围都没有找到第n+1个字符,这时候只好在路径上回到第n-1的字符,重新定位第n个字符。
由于路径不能重复进入矩阵的格子,所以还需要定义和字符矩阵大小一样的布尔值矩阵,用来识别路径是否已经进入了某个格子。
private int pathLength = 0;
private boolean hasPath(String matrix, int rows, int cols, String str) {
if (matrix == null || matrix.length() != rows * cols || str == null) {
return false;
}
boolean[] visited = new boolean[matrix.length()];
pathLength = 0;
for (int row = 0; row < rows; row++) {
for (int col = 0; col < cols; col++) {
if (hasPathInner(matrix, rows, cols, row, col, str, visited)) {
return true;
}
}
}
return false;
}
private boolean hasPathInner(
String matrix, int rows, int cols, int row, int col, String str, boolean[] visited
) {
if (pathLength == str.length()) {
return true;
}
boolean hasPath = false;
if (row >= 0 && row < rows && col >= 0 && col < cols
&& matrix.charAt(row * cols + col) == str.charAt(pathLength)
&& !visited[row * cols + col]) {
pathLength++;
visited[row * cols + col] = true;
hasPath = hasPathInner(matrix, rows, cols, row, col - 1,
str, visited)
|| hasPathInner(matrix, rows, cols, row - 1, col,
str, visited)
|| hasPathInner(matrix, rows, cols, row, col + 1,
str, visited)
|| hasPathInner(matrix, rows, cols, row + 1, col,
str, visited);
if (!hasPath) {
pathLength--;
visited[row * cols + col] = false;
}
}
return hasPath;
}
6.3.2 (13)机器人的运动范围¶
地上有一个m行n列的方格。一个机器人从坐标(0, 0)的格子开始移动,它每一次可以向左、右、上、下移动一格,但不能进入行坐标和列坐标的数位之和大于k的格子。例如,当k为18时,机器人能够进入方格(35, 37),因为3+5+3+7=18。但它不能进入方格(35, 38),因为3+5+3+8=19。请问该机器人能够到达多少个格子?
和前面的题目类似,这个方格也可以看成\(m\times{n}\)的矩阵。同样,在这个矩阵中,除边界上的格子之外,其他格子都有4个相邻的格子。
机器人从坐标(0, 0)开始移动,当它准备进入(i, j)的格子时,通过检查坐标的位数来判断机器人是否可以进入。如果能够进入,则在判断它能否进入4个相邻的格子。因此,我们可以用如下的代码来实现回溯算法:
private int movingCount(int threshold, int rows, int cols) {
if (threshold < 0 || rows <= 0 || cols <= 0) {
return 0;
}
boolean[] visited = new boolean[rows * cols];
return movingCountInner(threshold, rows, cols, 0, 0, visited);
}
private int movingCountInner(int threshold, int rows, int cols, int x, int y, boolean[] visited) {
int index = rows * x + y;
int count = 0;
if (x >= 0 && x < cols && y >= 0 && y < rows && !visited[index] && isMatched(threshold, x, y)) {
visited[index] = true;
count =
movingCountInner(threshold, rows, cols, x - 1, y, visited)
+ movingCountInner(threshold, rows, cols, x, y - 1, visited)
+ movingCountInner(threshold, rows, cols, x + 1, y, visited)
+ movingCountInner(threshold, rows, cols, x, y + 1, visited)
+ 1;
}
return count;
}
private boolean isMatched(int threshold, int x, int y) {
int sum = 0;
do {
sum += x % 10;
x /= 10;
} while (x != 0);
do {
sum += y % 10;
y /= 10;
} while (y != 0);
return sum <= threshold;
}
6.4 动态规划与贪婪算法¶
如果题目是求一个问题的最优解(通常是求最大值或者最小值),而且该问题能够分解成若干个子问题,而且子问题之间还有重叠的更小的子问题,就可以考虑使用动态规划来解决这个问题。
我们在应用动态规划之前要分析能够把大问题分解为小问题,分解后的每个小问题也存在最优解。如果把小问题的最优解组合起来能够得到整个问题的最优解,那么我们可以应用动态规划来解决这个问题。
例如第14题中,我们如何长度为n的绳子剪成若干段,使得得到的各段长度的乘积最大。这个问题的目标是求出各段绳子长度的乘积最大值,也就是 求一个问题的最优解 ——这是可以应用动态规划求解的问题的第一个特点。
我们把长度为\(n\)的绳子剪成若干段后得到的乘积最大值定义为函数\(f(n)\)。假设我们把第一刀减在长度为\(i(0< i < n)\)的位置,于是把绳子剪成了长度分别为i和n-i的两段。我们想要得到整个问题的最优解\(f(n)\),那么要同样用最优化的方法把长度为i和n-i的两段分别剪成若干段,使得它们各自剪出的每段绳子的长度乘积最大。也就是说 整体问题的最优解是依赖各个子问题的最优解 ——这是可以应用动态规划求解的问题的第二个特点。
我们把大问题分解为若干个小问题,这些小问题之间还有相互重叠的更小的子问题 ——这是可以应用动态规划求解的问题的第三个特点。假设绳子最初的长度为10,我们可以把绳子剪成长度分别为4和6的两段,也就是\(f(4)\)和\(f(6)\)都是\(f(10)\)的子问题。接下来分别求解这两个子问题,我们可以把长度为4的绳子剪成均为2的两段,即\(f(2)\)是\(f(4)\)的子问题。同样,我们也可以把6剪成2和4的两段,即\(f(2)\)和\(f(4)\)都是\(f(6)\)的子问题。我们注意到\(f(2)\)是\(f(4)\)和\(f(6)\)公共的更小的子问题。
由于子问题在分解大问题的过程中重复出现,为了避免重复求解子问题,我们可以用从下往上的顺序先计算小问题的最优解并存储下来,再以此为基础求取大问题的最优解。 从上往下分析问题,从下往上求解问题 ,这是可以应用动态规划求解的问题的第四个特点。在大部分题目中,已解决的子问题的最优解都存储在一维或者二维数组中。
在应用动态规划时,我们每一步都可能面临若干个选择。在求解第14题时,我们在剪一刀的时候就有n-1个选择。我们可以剪在任何位置,由于我们事先不知道剪在哪个位置是最优的解法,只好把所有的可能都尝试一遍,然后得出最优的剪法。
贪婪算法和动态规划不一样。当我们应用贪婪算法时,每一步都可以做出一个贪婪选择,基于这个选择,我们确定能够得到最优解。为什么贪婪选择能够得到最优解,这是我们应用贪婪算法时都需要问的问题,需要用数学方式来证明贪婪选择是正确的。
6.4.1 (14)剪绳子¶
给你一根长度为n绳子,请把绳子剪成m段(m、n都是整数,n>1并且m≥1)。每段的绳子的长度记为k[0]、k[1]、……、k[m]。k[0]*k[1]*…*k[m]可能的最大乘积是多少?例如当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到最大的乘积18。
解法一:动态规划
private int maxProductAfterCutting_solution1(int length) {
if (length < 2) {
return 0;
} else if (length == 2) {
return 1;
} else if (length == 3) {
return 2;
}
int[] products = new int[length + 1];
products[0] = 0;
products[1] = 1;
products[2] = 2;
products[3] = 3;
for (int i = 4; i <= length; i++) {
int max = 0;
for (int j = 1; j <= i / 2; j++) {
int result = products[j] * products[i - j];
if (result > max) {
max = result;
}
products[i] = max;
}
}
return products[length];
}
解法二:贪婪算法
我们按照如下的策略来剪绳子,则得到的各段绳子的长度的乘积最大:当n>=5时,我们尽可能多地剪长度为3的绳子;当剩下的绳子长度为4时,把绳子剪成两段长度为2的绳子。
private int maxProductAfterCutting_solution2(int length) {
if (length < 2) {
return 0;
} else if (length == 2) {
return 1;
} else if (length == 3) {
return 2;
}
// 尽可能多剪去长度为3的绳子段
int timesOf3 = length / 3;
// 当绳子最后剩下的长度为4时,不能再减去长度为3的绳子段
if (length - timesOf3 * 3 == 1) {
timesOf3--;
}
// 此时更好的方法是把绳子剪成长度为2的两段,因为2x2>3x1
int timesOf2 = (length - timesOf3 * 3) / 2;
return (int) Math.pow(3, timesOf3) * (int) Math.pow(2, timesOf2);
}
接下来我们证明这种思路的正确性。首先,当n>=5时,我们可以证明2(n-2)>n并且3(n-3)>n。也就是说,当绳子剩下的长度大于或者等于5的时候,我们就把它剪成长度为3或者2的绳子段。另外,当n>=5时,3(n-3)>=2(n-2),因此我们应该尽量多剪长度为3的绳子段。
前面证明的前提是n>=5。那么当绳子的长度为4时,2x2>3x1,同时2x2=4,也就是说当绳子长度为4时其实没必要剪,只是题目要求至少一刀。
6.5 位运算¶
位运算只有5种运算:与、或、异或、左移、右移。
与、或、异或运算的规律可以用下表总结:
| 与(&) | 0 & 0 = 0 | 1 & 0 = 0 | 0 & 1 = 0 | 1 & 1 = 1 |
| 或(|) | 0 | 0 = 0 | 1 | 0 = 1 | 0 | 1 = 1 | 1 | 1 = 1 |
| 异或(^) | 0 ^ 0 = 0 | 1 ^ 0 = 1 | 0 ^ 1 = 1 | 1 ^ 1 = 0 |
左移运算符m<<n表示把m左移n位。在左移n位的时候,最左边的n位会被丢弃,同时在最右边补上n个0。比如:
00001010 << 2 = 00101000
10001010 << 3 = 01010000
右移运算符m>>n表示把m右移n位。在右移n位的时候,最右边的n位将被丢弃。但右移时处理最左边位的情形要稍微复杂一点。如果数字是一个无符号数值,则用0填补最左边的n位;如果数字是一个有符号数值,则用数字的符号位填补最左边的n位。也就是说,如果数字原先是一个正数,则右移之后再最左边补n个0;如果数字原先是个负数,则右移之后再最左边补n个1。下面是对两个8位有符号数进行右移的例子:
00001010 >> 2 = 00000010
10001010 >> 3 = 11110001
6.5.1 (15)二进制中1的个数¶
请实现一个函数,输入一个整数,输出该数二进制表示中1的个数。例如把9表示成二进制是1001,有2位是1。因此如果输入9,该函数输出2。
解法一:常规解法
先判断整数二进制表示中最右边一位是不是1;然后把输入的整数右移一位,此时原来处于从右边数起的第二位被移到最右边了,再判断它是不是1;这样一直移动,直到整个整数变成0为止。现在的问题变成了怎么判断一个整数的最右边是不是1。这也很简单,只需要把整数和1做位与运算看结果是不是0就知道了。
但是,如果输入一个负数,比如0x80000000,则运行的时候会发生什么情况?当把负数0x80000000右移一位的时候,并不是简单地把最高位的1移到第二位变成0x4000000,而是0xC000000。这是因为移位前是一个负数,仍然要保证移位后也是一个负数,因此移位后的最高位会设为1。如果一直做右移运算,那么最终这个数字就会变成0xFFFFFFFF而陷入死循环。
为了避免死循环,我们可以不右移输入的数字n。而是左移一个flag。
int NumberOf1_Solution1(int n) {
int count = 0;
int flag = 1;
while (flag != 0) {
if ((n & flag) != 0) {
count++;
}
flag = flag << 1;
}
return count;
}
解法二:牛逼解法
我们发现,把一个整数减去1,再和原整数做位与运算,会把该整数最右边的1变成0。比如下面两个例子
1100 -> (1011 & 1100) = 1000 -> 0
1010 -> (1001 & 1010) = 1000 -> 0
int NumberOf1_Solution2(int n) {
int count = 0;
while (n != 0) {
count++;
n = (n - 1) & n;
}
return count;
}
相关题目
用一条语句判断一个整数是不是2的整数次方。
一个整数如果是2的整数次方,那么它的二进制位表示中有且只有一位是1,而其他所有位都是0。根据前面的分析,把这个整数减去1之后再和它自己做与运算,这个整数中唯一的1就会变成0
相关题目
输入两个整数m和n,计算需要改变m的二进制表示中的多少位才能得到n。比如10的二进制表示为1010,13的二进制表示为1101,需要改变1010中的3位才能得到1101。
我们可以分为两步解决这个问题:第一步求这两个数的异或;第二步统计异或结果中1的位数
举一反三
把一个整数减去1之后再和原来的整数做位与运算,得到的结果相当于把整数的二进制表示中最右边的1变成0。很多二进制问题都可以用这种思路解决。
7. 总结¶
数据结构题目一直是考查的重点。数组和字符串是两种最基本的数据结构。链表是使用频率最高的一种数据结构。如果想加大面试的难度,那么他很有可能会选用与树相关的题目。由于栈和递归调用密切相关,队列在图(包括树)的宽度优先遍历中需要用到,因此也需要掌握这两种数据结构。
算法是另一个重点。查找(特别是二分查找)和排序(特别是快速排序和归并排序)是经常考查的算法。回溯法很适合解决迷宫以及类似的问题。如果需要求一个问题的最优2解,那么可以尝试使用动态规划。假如我们在用动态规划分析问题时发现每一步都存在一个能得到最优解的选择,那么可以尝试使用贪婪算法。另外,我们还需要掌握分析时间复杂度的方法,理解即使同一思路,基于循环和递归的不同实现,它们的时间复杂度可能不大相同。很多时候我们会用自上而下的递归思路分析问题,却会基于自下而上的循环实现代码。
位运算是针对二进制数字的运算规律。只要熟练掌握了二进制的与、或、异或、左移、右移操作,就能解决相关问题。